词法分析

词法分析器的作用

读入字符流, 组成词素, 输出词法单元序列.

将词素添加到 符号表 中

过滤空白, 换行, 制表符, 注释等
简化编译器的设计
模块化设计, 增强编译器的可移植性

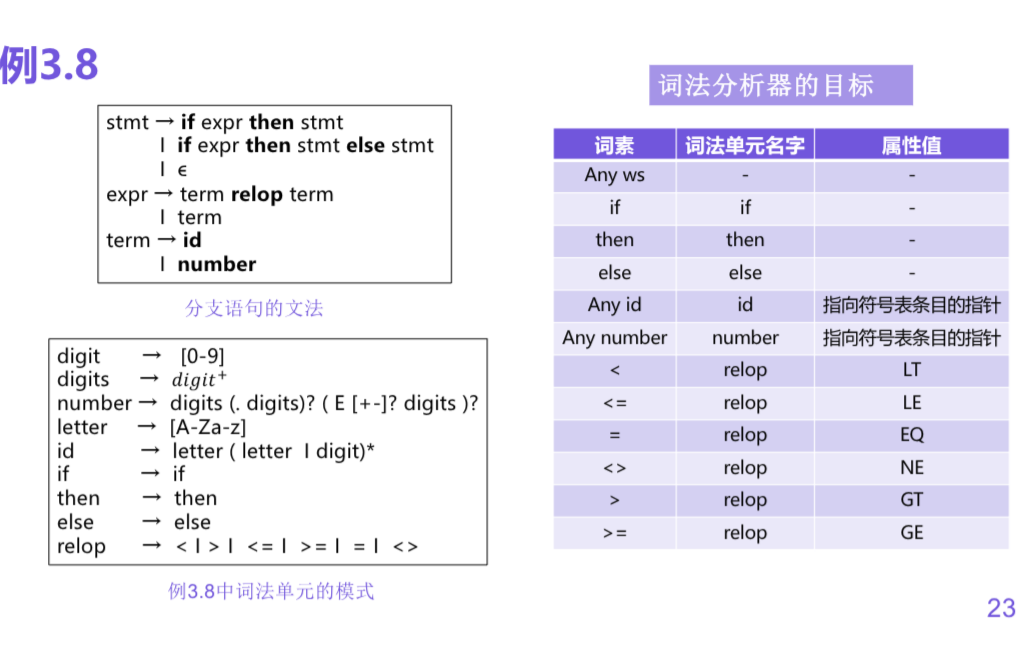
词法单元, 模式, 词素

词法单元(Token)

<词法单元名, 属性值>

词法单元名是表示词法单位种类的抽象符号, 语法分析器通过单元名即可确定词法单元序列的结构
属性值通常用于语义分析之后的阶段

eg: <if, ->, <id, "counter">, <num, 100>

属性

一个模式匹配多个词素时, 必须通过属性来传递附加的信息

属性值将被用于语义分析, 代码生成等

不同的目的需要不同的属性

属性值通常是一个结构化数据
如词法单元id的属性: id内容, 类型, 第一次出现的位置...

词法错误

词法分析器本身很难发现源代码的错误, 如fi(true)无法判断fi是if写错了, 还是有fi这个函数.

词法分析器会返回id词法单元给语法分析器处理.

当所有模式都无法和剩余输入的某个前缀匹配时:

词法分析器不能继续处理输入
错误恢复策略
- 从剩余的输入中删除一个字符
- 向生育的输入中插入一个遗漏的字符
- 用一个字符来替换另一个字符
- 交换两个相邻的字符

模式(Pattern)

描述了一类词法单元的词素可能具有的形式

词素(Lexeme)

源程序中的字符序列

它和某个词法单元的模式匹配, 被词法分析器识别为该词法单元的实例

eg:

printf("Total = %d\n", score);

printf和score与标识符id的模式匹配
"Total = %d\n"与literal的模式匹配

词法单元	非正式描述	词素示例
if	字符i,f	if
comparison	<或>,<=,=>,==,!=	<=,!=
id	字母开头的字母/数字串	Pi,score,D2
number	任何数字常量	123
literal	在两个"之间,除"以外的任何字符	"Hello, World!\n"

词法单元的规约(正则表达式)

正则表达式可以高校简洁地描述处理词法单元时用到的模式类型

串和语言

字母表: 一个有穷的符号集合
- eg: 字母, 数字, 标点符号
- {0, 1}, Unicode
- 理论上, 任意的有限集合都可以看作是字母表
字母表上的串(string)是该表中符号的有穷序列
- 串s的长度是指s中符号出现的次数
- 空串ε的长度为0
语言是某个给定字母表上的串的可数集合
前缀: 从串的尾部删除任意个符号后得到的串
后缀: 从串的开始处删除任意个符号后得到的串
子串: 删除串中的某个前缀和某个后缀后得到的串
真前缀/真后缀/真字串: 不等于原串或空串的前缀/后缀/子串
子序列: 从串中删除任意个符号后得到的串
串的运算
- 连接: x和y的连接是把y附加到x的后面, 记作xy.
x=dog, y=house, 则xy=doghouse
- 指数运算: x^n表示n个x连接在一起, x^0=ε
x=ha, 则x^3=hahaha
语言的运算
- 并: $L \cup M = {s | s \in L or s \in M}$
- 连接: $L M = {x y | x \in L and y \in M}$
- 克林闭包: $L^{*} = ⋃_{n \geq 0} L^{n}$
- 正闭包: $L^{+} = ⋃_{n \geq 1} L^{n}$

正则表达式

将 $L (L \cup D)^{*}$ 当作表示标识符的集合, 可以给出字母, 数位集合的名字, 再用并, 连接, 闭包等运算来描述标识符, 就得到了正则表达式.

eg:

l e t t e r (l e t t e r | d i g i t)^{*}

定义

字母表Σ上的正则表达式的定义

L(r)表示正则表达式r所表示的语言
基本部分
- ε是正则表达式, L(ε)={ε}
- 如果a是Σ中的一个符号, 则a是正则表达式, L(a)={a}
归纳步骤
- 选择: (r)|(s), L((r)|(s))=L(r) ∪ L(s)
- 连接: (r)(s), L((r)(s))=L(r)L(s)
- 闭包: $(r)^{*}, L ((r)^{*}) = (L (r))^{*}$
- 括号: (r), L((r))=L(r)
运算优先级: * > 连接 > |
正则语言: 可以用一个正则表达式定义的语言

eg:

字 母 表 \sum = {a, b}

L (a | b) = {a, b}

L ((a | b) (a | b)) = {a a, a b, b a, b b}

L (a^{*}) = {ϵ, a, a a, a a a, a a a a, . . .}

正则定义

为了方便书写, 可以给正则表达式命名, 形成正则定义.

正则定义是如下形式的定义序列

d_1 -> r_1
d_2 -> r_2
...
d_n -> r_n

其中,

其中, d_i不在 $\sum$ 中且各不相同.
每个r_i是字母表 $\sum \cup {d_{1}, d_{2}, . . ., d_{- 1}}$ 上的正则表达式, 这保证了不会出现递归定义

eg:

在C语言中:

letter -> A | B | ... | Z | a | b | ... | z | _
digit -> 0 | 1 | ... | 9
id -> letter (letter | digit)*

扩展

基本运算符: 选择, 连接, 闭包
扩展运算符
- 一个或多个实例: 单目后缀+
  - r+ = rr*
- 零个或一个实例: 单目后缀?
  - r? = (r | ε)
- 字符类
  - $[a_{1}, a_{2}, . . ., a_{n}]$ 等价于 $(a_{1} | a_{2} | . . . | a_{n})$
  - $[a - z]$ 等价于 $(a | b | . . . | z)$

使正则表达式更简洁, 对描述能力无影响

正则表达式与词法单元的识别

正则表达式可以用来描述词法单元的模式, 首先通过正则定义来描述各种词法单元的模式.

eg: C语言中的标识符

letter -> A | B | ... | Z | a | b | ... | z | _
digit -> 0 | 1 | ... | 9
id -> letter (letter | digit)*

当词法分析器识别到某种模式时, 不返回词法单元, 继续识别其它模式

eg:

词法单元的识别(状态转换图)

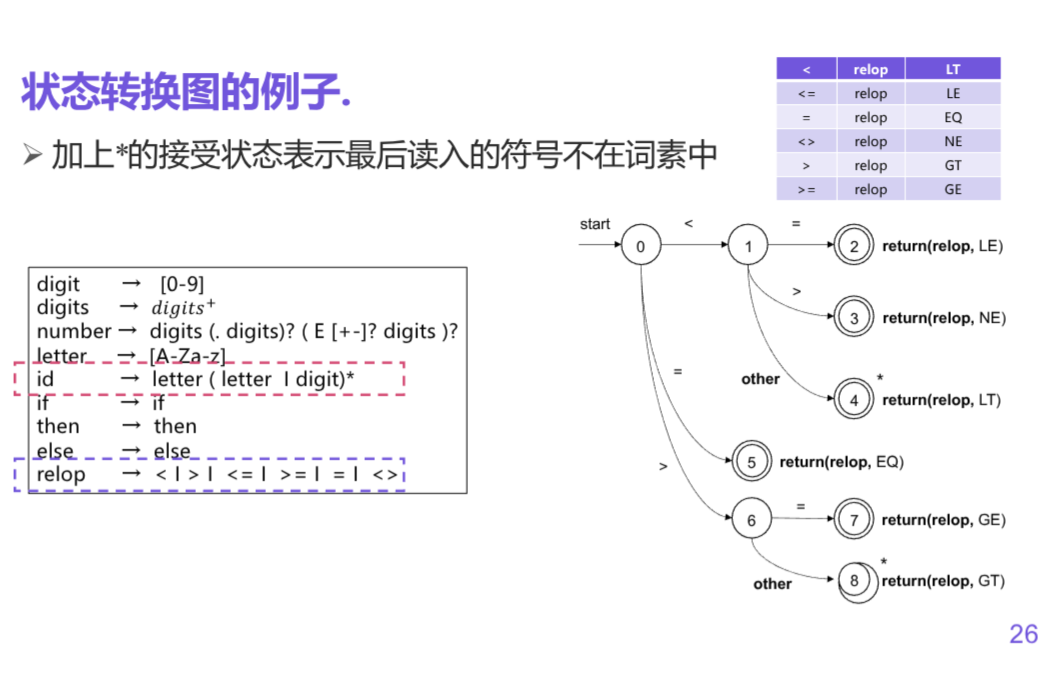
状态转换图(Transition Diagram)

词法分析器的重要组件之一

点[状态(state)]: 表示在识别词素时可能出现的情况
- 状态看作是已处理部分的总结[lexicalBegin指针和forward指针之间的内容]
- 某些状态为接受状态或最终状态, 表示已经识别出一个词素
- 开始状态(初始状态): 用Start边表示
边[转换(Transition)]: 从一个状态指向另一个状态
- 边的标号是一个或多个符号
- 当前状态为s, 下一个输入符号为a, 就沿着从s离开, 标号为a的边到达下一个状态

eg:

保留字与标识符的识别

保留字一般也符合标识符的模式, 比如if符合变量的标识符模式letter(letter | digit)*.

解决办法:

在符号表中先填保留字, 并表明它们不是普通标识符
为保留字建立独立的, 高优先级的状态转换图

从转换图构造词法分析器

构造词法分析器的一般步骤:

变量state记录当前状态

一个switch根据state转到相应的代码

每个状态对应一段代码:

这段代码根据读入的符号, 确定下一个状态
如果找不到相应的边, 则调用fail()进行错误恢复

进入某个接受状态时, 返回相应的词法单元

如果状态有*标记, 需要回退forward指针

本质是一个状态机的实现

eg:

Token getRelop() {
    TOKEN retToken = new(RELOP);
    while (1) {
        switch (state) {
            case 0:
                c = nextChar();
                switch (c) {
                    case '<':
                        state = 1;
                        break;
                    case '>':
                        state = 6;
                        break;
                    case '=':
                        state = 5;
                        break;
                    default:
                        fail();
                }
                break;
            case 1:
                // ...
            case 8:
                retract(); // *, 回退一个字符
                retToken.attribute = GT;
                return retToken;
        }
    }
}

词法分析器生成工具及设计

词法分析工具Lex/Flex

Lex/Flex是Unix系统下的词法分析器生成工具,

支持用regexp描述词法单元的模式, 给出一个词法分析器的规约
输入表示: Lex语言
工具本身: 是一个编译器, 将Lex语言的规约翻译成C代码
核心: 将输入的模式 -> 状态转换图, 并生成代码

通常和YACC/Bison一起使用, 生成编译器的前端

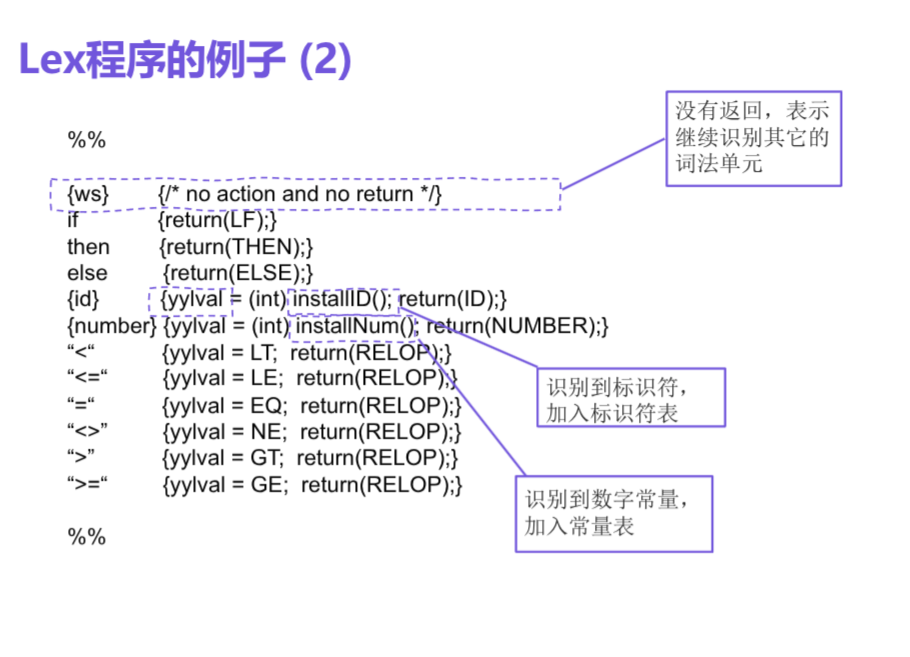
Lex源程序的结构

声明部分
- 常量: 表示常数的标识符
- 正则定义
转换规则
- 模式
  - 模式是正则表达式
  - 动作表示识别到相应模式时应采取的处理方式
  - 处理方式通常是用C语言代码表示
辅助函数
- 各个动作中使用的函数

声明部分
%%
转换规则
%%
辅助函数

%{
#include "token.h"
%}
digit   [0-9]
letter  [A-Za-z]
id      {letter}({letter}|{digit})**
%%
"if"        { return newToken(IF); }
"else"      { return newToken(ELSE); }
{ id }      { return newIdToken(IDENTIFIER, yytext); }
{ digit }+  { return newNumToken(NUMBER, atoi(yytext)); }
[ \t\n]    { /* 忽略空白符 */ }
.          { printf("未知符号: %s\n", yytext); }
%%
int yywrap() {
    return 1;
}
// ...

%{和}%之间的内容一般会被直接复制到生成的lex.yy.c中. 辅助函数也会被复制到lex.yy.c中.

Lex中冲突解决方法

冲突: 多个输入前缀与某个模式相匹配, 或者一个前缀与多个模式匹配

方法:

多个前缀可能匹配时, 选择最长的前缀

eg
输入: <= 模式: <和<= 选择<=

一个前缀和多个模式匹配时, 选择列在前面的模式

eg
输入: if 模式: if和标识符id 选择if

有穷自动机

本质上和状态转换图相同, 但有穷自动机只回答Yes/No问题: 输入串是否属于某个语言

分为两类

不确定的有穷自动机(Nondeterministic Finite Automaton, NFA): 边上的标号没有限制, 一个符号可出现在离开同一个众泰的多条边上, ε可以做标号
确定的有穷自动机(Deterministic Finite Automaton, DFA): 对于每个状态以及每个符号, 有且仅有一条边(或者最多只有一条边)

两种自动机都识别正则语言, 每个可以用正则表达式描述的语言都可以用NFA或者DFA识别
识别: 判定一个串是否属于对应正则语言(Yes/No)

不确定的有穷自动机

NFA:

一个有穷的状态集合S
一个输入符号字母表 $\sum$ (input alphabet)
转换函数(Transition function)对于每个状态和 $\sum \cup {ϵ}$ 中的符号, 给出相应的后续状态集合
S中的某个状态 $s_{0}$ 被指定为开始状态/初始状态(有些定义中可以有多个开始状态)
S的一个子集F被指定为接受状态集合

状态集合: S={0, 1, 2, 3}
输入字母表: $\sum$ ={a, b}
开始状态: s0=0
接受状态集合: F={3}
转换函数:
- δ(0, a)={0, 1}
- δ(0, b)={0}
- δ(1, a)={2}
- δ(2, b)={3}

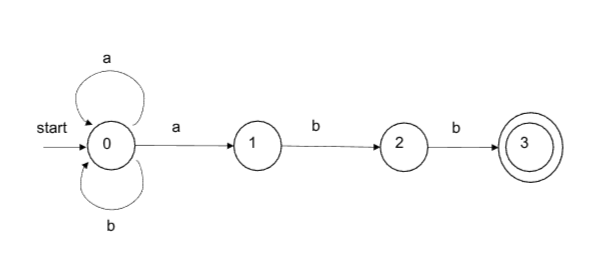
转换表表示法

可以用二维表表示NFA的转换函数

每行对应一个状态
每列对于于一个输入符号或ε
每个条目表示对应的后继状态集合

State	a	b	ε
0	{0, 1}	{0}	{}
1	{2}	{}	{}
2	{}	{3}	{}
3	{}	{}	{}

输入字符串的接受

输入字符串x

iff对应的转换图中存在一条从开始状态到某个接受状态的路径, 且该路径各条边上的标号按顺序组成x(不含ε)

NFA接受的语言: 从开始状态到达接受状态的所有可能路径的标号串的集合

L((a|b)+abb) eg:

输入字符串abb
- 存在路径0 --a--> 1 --b--> 2 --b--> 3
- 因为存在一条路径到达接受状态3, 所以NFA接受字符串abb

从正则表达式到自动机

正则表达式: 简介精确地描述词法单元的模式
自动机: 便于机器执行的计算模型
- NFA: 易于从正则表达式转换(3跳转)
- DFA: 可由NFA转换, 便于机器高效模拟执行
  - DFA最小化, 优化空间使用率

正则表达式 -> NFA -> DFA

正则表达式 -> NFA

基本思想

根据正则表达式的递归定义, 安装正则表达式的结构递归地构造出相应的NFA
算法分成两个部分
- 基本规则处理 $ϵ$ 和单个符号的情况
- 对于每个正则表达式的运算, 建立组合相应NFA的方法

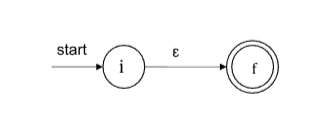
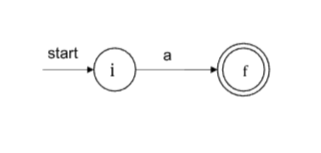
转换算法 1.

基本规则
- r=ε

r=a, a∈ $\sum$

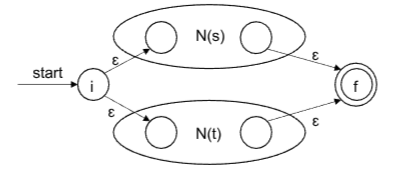
归纳部分
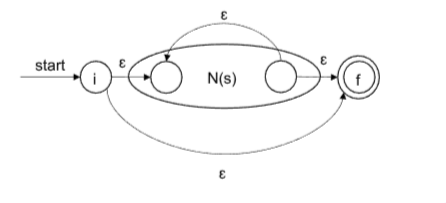
r=s|t

r=st

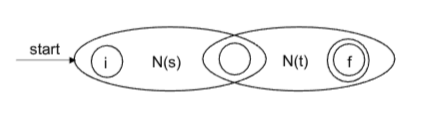
r=s*

eg:

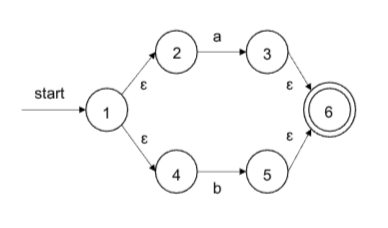
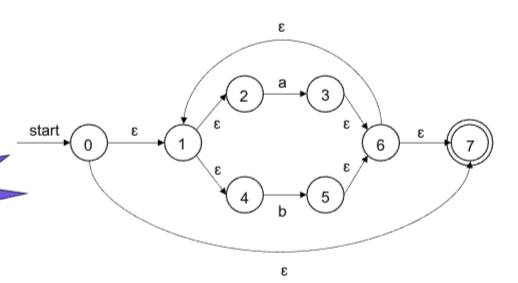
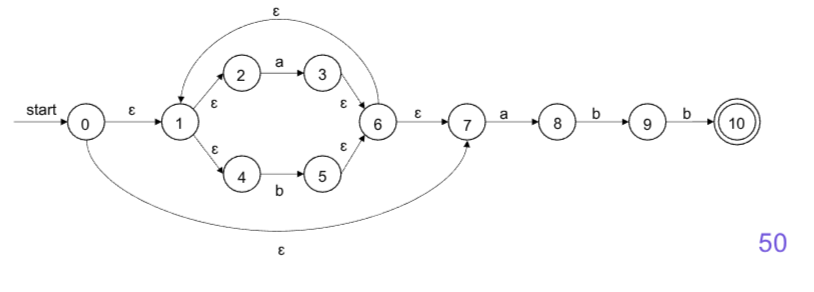
L((a|b)*abb)

拆解+合并

第一个a对应的NFA

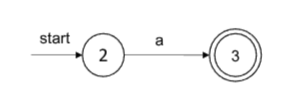
第一个b对应的NFA

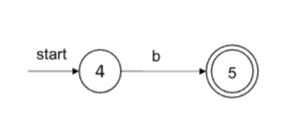
(a|b)对应的NFA

(a|b)*对应的NFA

(a|b)*abb对应的NFA

确定的有穷自动机

NFA的不确定性导致它不易模拟

维护多个状态
跟踪多条路径

一个NFA被称为DFA, 如果

没有标号ε的转换
对于每个状态s和每个输入符号a, 有且仅有一条标号为a的离开s的边

每个NFA都有一个等价的DFA

DFA的模拟运行

s = s0;
c = nextChar();
while (c != eof) {
    s = move(s, c);
    c = nextChar();
}

if (s在F中) return "Yes";
else return "No";

move给出了离开状态s且标号为c的边的目标状态

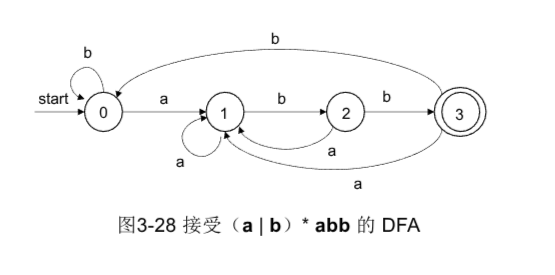
先前的例子改造成DFA长这样

从NFA到DFA

子集构造法

基本思想

构造得到的DFA的每个状态和NFA的状态子集对应
DFA读入 $a_{1}, a_{2}, . . ., a_{n}$ 后到达的状态对应于NFA开始状态出发验证 $a_{1}, a_{2}, . . ., a_{n}$ 可能到达的状态集合
在算法中"并行地模拟"NFA在遇到一个给定输入串时可能执行的所有动作

目标DFA每个状态对应一个NFA状态集合
目标DFA状态之间的转换对应NFA状态集合之间的转换
理论上, 最坏情况下DFA的状态个数是NFA状态个数的指数多个( $2^{n}$ )

但大部分应用, NFA和相应DFA的状态数量大致相同

算法中使用到的基本操作
- ε-closure(s): 从NFA状态s开始, 只通过ε转换能到达的NFA状态集合
- ε-closure(T): 枚举T中所有状态, 从T中某个状态s开始, 只通过ε转换能到达的NFA状态集合
- move(T, a): 枚举T中所有状态, 从T中某个状态s出发, 通过一个标号为a的转换能到达的NFA状态集合

ε-closure(T)算法: 图搜索过程

// 将T的所有状态压入stack中
// 将e-closure(T)初始化为T
while (!stack.empty()) {
    t = stack.pop();
    for (每个满足如下条件的u: 从t出发有一个标号为ε的转换到达状态u) {
        if (u不在ε-closure(T)中) {
            将u加入到ε-closure(T)中
            将u压入栈中
        }
    }
}

ε-closure(s0)算法

$D_{s t a t e s}$ : DFA状态, 每个元素对应一个NFA状态集合
$D_{t r a n}$ : DFA状态转移表

// 一开始, ε-closure(s0)是Dstates中的唯一状态, 且它未加标记
// 加标记=visited
while (在Dstates中有一个未标记状态T) {
    给T加上标记;
    for (每个输入符号a) {
        U = ε-closure(move(T, a));
        if (U不在Dstates中) {
            将U加入到Dstates中, 且不加标记;
        }
        Dtran[T, a] = U;
    }
}

eg:

对于之前的L((a|b)*abb)

初始化DFA

找出开始状态能通过ε转换到达的所有状态 S0 = ε-closure(0) = {0, 1, 2, 4, 7}

逐个输入符号对S0, 输入a:

// move(T, a): 遍历T中所有状态, 找出通过a转换能到达的状态集合 move(S0, a) = {3, 8} // 2 --a->3, 7 --a->8

S1 = ε-closure(move(S0, a)) = {1, 2, 3, 4, 6, 7, 8} // 3和8经过0个ε转换到达自身

对S0, 输入b:

move(S0, b) = {5}

S2 = ε-closure(move(S0, b)) = {1, 2, 4, 5, 6, 7}

重复上述过程, 直到没有未标记状态

对S1, 输入a:

move(S1, a) = {3, 8} // 重复

对S1, 输入b:

move(S1, b) = {5, 9}

S4 = ε-closure(move(S1, b)) = {1, 2, 4, 5, 6, 7, 9}

对S2, 输入a:

move(S2, a) = {3, 8} // 重复

对S2, 输入b:

move(S2, b) = {5} // 重复

对S4, 输入a:

move(S4, a) = {3, 8} // 重复

对S4, 输入b:

move(S4, b) = {5, 10}

S5 = ε-closure(move(S4, b)) = {1, 2, 4, 5, 6, 7, 10}

对S5, 输入a:

move(S5, a) = {3, 8} // 重复

对S5, 输入b:

move(S5, b) = {5} // 重复

因此最终DFA状态集合为:

S0 = {0, 1, 2, 4, 7}
S1 = {1, 2, 3, 4, 6, 7, 8}
S2 = {1, 2, 4, 5, 6, 7}
S4 = {1, 2, 4, 5, 6, 7, 9}
S5 = {1, 2, 4, 5, 6, 7, 10}

转换表为:

NFA状态	DFA状态	a	b
0,1,2,4,7	S0	S1	S2
1,2,3,4,6,7,8	S1	S1	S4
1,2,4,5,6,7	S2	S1	S2
1,2,4,5,6,7,9	S4	S1	S5
1,2,4,5,6,7,10	S5	S1	S2

画DFA图只需要关注DFA状态和输入a和b的情况

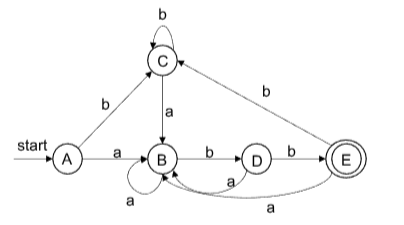
DFA状态数量最小化

DFA状态越少, 空间效率越高. 通过DFA的最小化可以得到状态数量最少的DFA(不计同构, 这样的DFA是唯一的)

可区分: 如果存在串x, 使得从状态s1和s2, 一个到达接受状态而另一个到达非接受状态, 那么x就区分了s1和s2.

如果存在某个串区分了s和t, 那么s和t是可区分的, 否则是不可区分的.

不可区分的两个状态就是等价的, 可以合并.

最小化算法(基本思想)

把所有可区分状态分开(迭代过程)
- 基本步骤: ε区分了接受状态和非接受状态
- 归纳步骤: 如果状态s和t是可区分的, 且s'到s, t'到t有标号为a的边, 那么s'和t'也是可区分的
最终没有区分开的状态就是等价的
- 所有的死状态都是等价的
从划分的等价类中选取代表, 重建DFA

划分部分

设置初始划分 $Π = {S - F, F}$
迭代, 枚举字母表, 不断划分等价类

for (Π中的每个元素G) {
    细分G, 使得G中的两个状态s和t在同一小组中iff对所有的输入符号a都到达Π中的同一组;
    Πnew = 将Π中的G替换为细分得到的小组;
}

如果 $Π_{n e w} == Π$ , 令 $Π_{f i n a l} = Π$ , 否则令 $Π = Π_{n e w}$ , 重复步骤2

在 $Π_{f i n a l}$ 的每个组中选择一个状态作代表, 作为最小化DFA的状态

开始状态就是包含原开始状态的组的代表
接受状态就是包含原接受状态的组的代码(这个组一定只包含接受状态)

转换关系构造如下

如果s是G的代表, 而原DFA中s在a上的转换到达t, 且t所在组的代表为r, 那么最小化DFA中有从s到r的在a上的转换

eg:

对于之前的DFA: {A, B, C, D, E} // S0, S1, S2, S3, S4

初始划分

得到{{A, B, C, D}, {E}}

把接受状态分开

处理{A, B, C, D}

输入a:

A, B, C, D都到达B

同组不分

输入b:

A到达C
B到达D
C到达C
D到达E

D到达了接受状态, 分组

得到{{A, B, C}, {D}, {E}}

处理{A, B, C}

输入a:

A到达B
B到达B
C到达B

同组不分

输入b:

A到达C
B到达D
C到达C

D不在{A, B, C}内, 分组

得到{{A, C}, {B}, {D}, {E}}

处理{A, C}

输入a:

A到达B
C到达B

同组

输入b:

A到达C
C到达C

同组

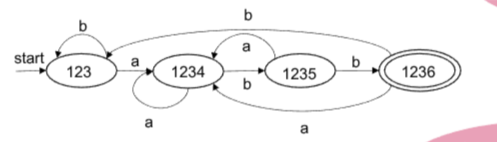
最终划分为{{A, C}, {B}, {D}, {E}}

选取A, B, D, E作为代表

状态	a	b
A	B	A
B	B	D
D	B	E
E	B	A

重建DFA:

自动机到词法分析器

正则表达式: 识别单个模式
词法分析器: 识别多种模式

关键字, 运算符, 标识符, 数字...

NFA合并方法:

引入新的开始状态, 并引入从该开始状态到各个原开始状态的ε转换
得到的NFA所接受的语言是原来各个NFA语言的并集
不同的接受状态代表不同的模式

对得到的NFA进行确定话, 得到DFA

一个DFA的接受状态对应于NFA的状态子集, 其中至少包括一个NFA的接受状态.

如果其中包括多个对应不同模式的NFA接受状态, 则表示当前的输入前缀对应于多个模式, 存在冲突
需要找出第一个这样的模式, 将该模式作为此DFA接受状态的输出

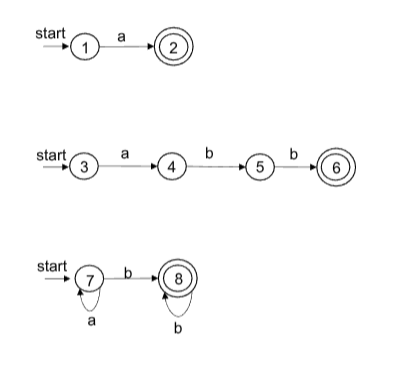
eg:

假设有三个模式

模式1: a
模式2: abb
模式3: a*b+

构造各模式的NFA

合并NFA

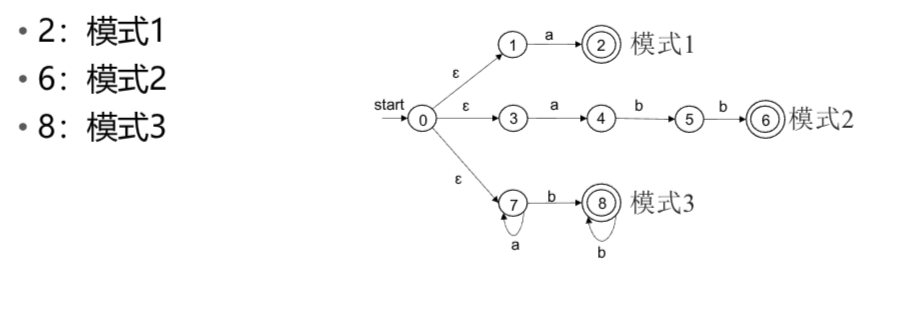
确定化

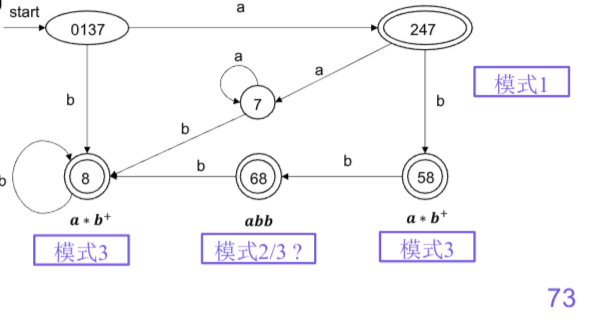
abb和a*b+都在状态68接受了.

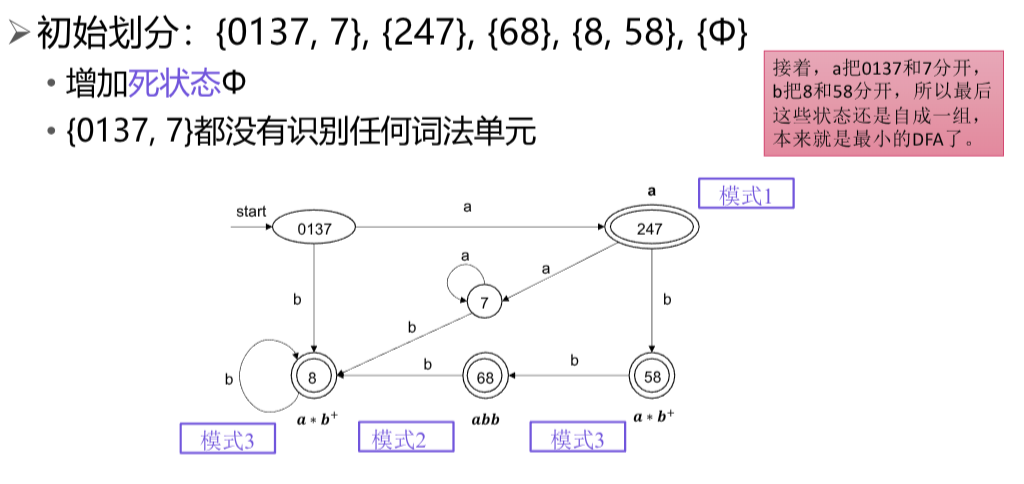
词法分析器状态的最小化

基本思想与DFA最小化算法相同

差异

词法分析器中的接受状态对应于不同的模式
对应不同模式的接受状态不一定是等价的
初始划分为
- 所有非接受状态集合+对应各模式的接受状态集合
其余划分和构造的方法均相同
接受状态对应的模式就是原来的模式

eg:

词法分析 ​

词法分析器的作用 ​

词法单元, 模式, 词素 ​

词法单元(Token) ​

属性 ​

词法错误 ​

模式(Pattern) ​

词素(Lexeme) ​

词法单元的规约(正则表达式) ​

串和语言 ​

正则表达式 ​

定义 ​

正则定义 ​

扩展 ​

正则表达式与词法单元的识别 ​

词法单元的识别(状态转换图) ​

状态转换图(Transition Diagram) ​

保留字与标识符的识别 ​

从转换图构造词法分析器 ​

词法分析器生成工具及设计 ​

词法分析工具Lex/Flex ​

Lex源程序的结构 ​

Lex中冲突解决方法 ​

有穷自动机 ​

不确定的有穷自动机 ​

转换表表示法 ​

输入字符串的接受 ​

从正则表达式到自动机 ​

正则表达式 -> NFA ​

确定的有穷自动机 ​

DFA的模拟运行 ​

从NFA到DFA ​

子集构造法 ​

DFA状态数量最小化 ​

最小化算法(基本思想) ​

自动机到词法分析器 ​

词法分析器状态的最小化 ​

词法分析

词法分析器的作用

词法单元, 模式, 词素

词法单元(Token)

属性

词法错误

模式(Pattern)

词素(Lexeme)

词法单元的规约(正则表达式)

串和语言

正则表达式

定义

正则定义

扩展

正则表达式与词法单元的识别

词法单元的识别(状态转换图)

状态转换图(Transition Diagram)

保留字与标识符的识别

从转换图构造词法分析器

词法分析器生成工具及设计

词法分析工具Lex/Flex

Lex源程序的结构

Lex中冲突解决方法

有穷自动机

不确定的有穷自动机

转换表表示法

输入字符串的接受

从正则表达式到自动机

正则表达式 -> NFA

确定的有穷自动机

DFA的模拟运行

从NFA到DFA

子集构造法

DFA状态数量最小化

最小化算法(基本思想)

自动机到词法分析器

词法分析器状态的最小化